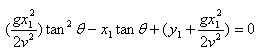
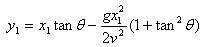
篮球比赛中，当运动员跳射投入三分球（空心球）时，往往会引来观众的啧啧称赞。那么运动员为何要跳起投篮呢？是为了动作的美感，是为了躲避防守队员，还是跳跃真的有助于投篮？
为了验证跳跃有助于投篮，就先得知道怎样才可使篮球容易进篮圈．
经测量，标准篮圈的直径为2R=45cm，而标准篮球的直径为d′=24.6cm．
设篮圈的面积为S，篮球最大的横切面积为s．
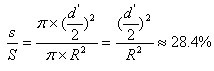
所以说，如果篮球是垂直穿过篮圈的，“空心球”应是件轻而易举的事．
但由于篮圈距地面有一定的高度，篮球须经抛物线才进入篮圈，篮球在入篮圈前一点与圈的平面所成的入射角j是很难接近90°的。从篮球的角度看，不同的j角会使篮圈呈现出不同的形状．
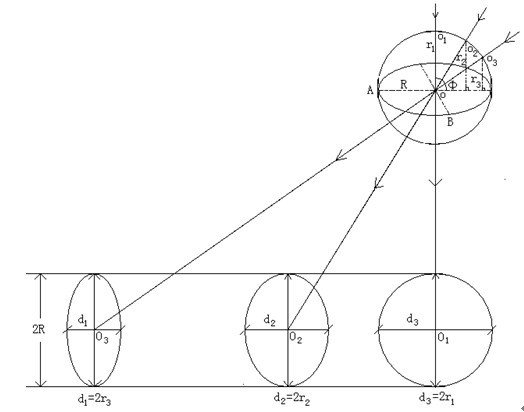
如上图，以O为圆心过AB的圆为篮圈，O1，O2，O3所在的面为垂直于篮圈所在的面，取篮球为质点，以O1O、O2O、O3O三条入射线投入篮中。对于篮球，篮圈呈现出如图三种不同的形态．
r为球心到篮圈所在面的垂直高度，R为篮圈半径
故有：R*sinj=r
要把篮球投入篮圈，则必有d=2r大于篮球本身直径d′,即d>d′
\d=2r=2Rsinj>d′
把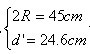
代入得 j >33.1°
由此可见当入射角j>33.1°时，入射角j越大篮球入篮的机会越大．
因为篮球是以抛物线进篮圈的，设如图篮球投出时速度为v与水平方向成θ°夹角；(x1 ,y1)为篮圈中心座标；t为整个投篮过程所需时间；则用斜抛公式，可知：
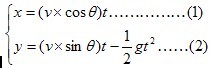
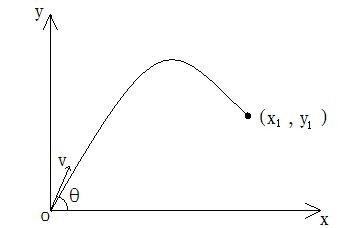
将(1)代入(2)得
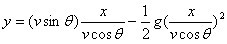
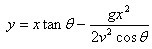
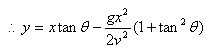
可知此函数为篮球运动的轨迹，要投篮成功，最好让球心经过(x1,y1),故代入(x1,y1),有
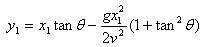
换成关于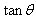
的方程
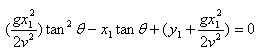
解之，得
，
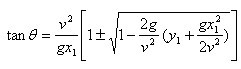又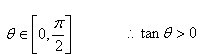 
又如前面所证θ>33.1°．
\只需考虑较大正根，故只取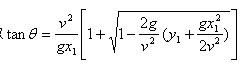
为方便讨论y1与θ的关系，设投篮者离篮底约4m,即x1=4m，并将球在离地面h处以v=8m/s的速度投射，经测量篮圈离地3.05m,可知y1=3.05m-h．
分取h1=1.85m h2=1.95m h3=2.05m h4=2.15m代入计算，结果如下：
(取g = 9.8 m/s2)
|
h |
y1=3.05-h |
θ |
|
1.85m |
1.2m |
67.9° |
|
1.95m |
1.1m |
68.3° |
|
2.05m |
1.0m |
68.6° |
|
2.15m |
0.9m |
68.9° |
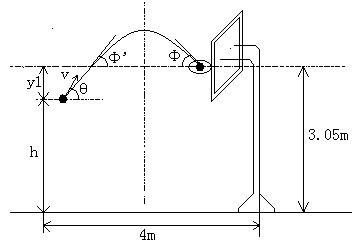
可知，跳起高度h越大，则投射角θ越大，j′就越大，根据二次函数图象的对称性，入射角j就越大。
又文章开头所证入射角越大，篮球入篮圈的几率就越大。
所以,跳跃有助于投“空心球”得证。